Mean Reversion in Bitcoin: Evaluating the Efficacy of Contrarian Entry Signals

In digital asset markets, where structural inefficiencies and high volatility dominate, mean-reversion strategies continue to attract attention as tactical overlays. This research note investigates whether systematically "buying the dip" in Bitcoin—defined by momentum-based oversold signals—can offer superior risk-adjusted returns compared to passive exposure.

Research Objective

Test Hypothesis: Does tactically entering long positions in BTC during RSI-based oversold regimes (e.g., RSI < 30) result in statistically superior performance vs. a buy-and-hold benchmark?

RSI signals vs. BTC price (2017-2024)

Signal Construction

✔ Entry: RSI < 30 (short-term capitulation)

✔ Exit: RSI > 50 (reversion to neutral)

✔ Capital: Full notional, no leverage

✔ Execution: Daily closes, zero fees/slippage

Python Implementation with vectorbt

import yfinance as yf
    import yfinance as yf
    import vectorbt as vbt
    import pandas as pd
    import numpy as np
    
    # Download BTC-USD spot price
    btc_price = yf.download('BTC-USD', start='2017-01-01', end='2024-01-01')['Close'].dropna()
    btc_price.name = 'BTC-USD'
    
    # Compute RSI (14-day window)
    rsi = vbt.RSI.run(btc_price, window=14)
    
    # Define entry/exit signals
    entries = rsi.rsi < 30
    exits = rsi.rsi > 50
    
    # Construct portfolio from signals
    portfolio = vbt.Portfolio.from_signals(
        btc_price,
        entries,
        exits,
        direction='long_only',
        init_cash=100_000,
        fees=0.0,
        slippage=0.0
    )
    
    # Performance metrics
    stats = portfolio.stats()
    print(stats)
    
    # Plot equity curve and drawdown
    print("Portfolio columns:", portfolio.wrapper.columns)
    
    if len(portfolio.wrapper.columns) == 1:
        col = portfolio.wrapper.columns[0]
        fig = portfolio.plot(title='Mean Reversion Strategy on BTC-USD', column=col)
    else:
        fig = portfolio.plot(title='Mean Reversion Strategy on BTC-USD')
    
    # Ajustar layout del gráfico para que no se tape el título
    fig.update_layout(
        title={'y': 0.95},
        margin=dict(t=180)
    )
    fig.show()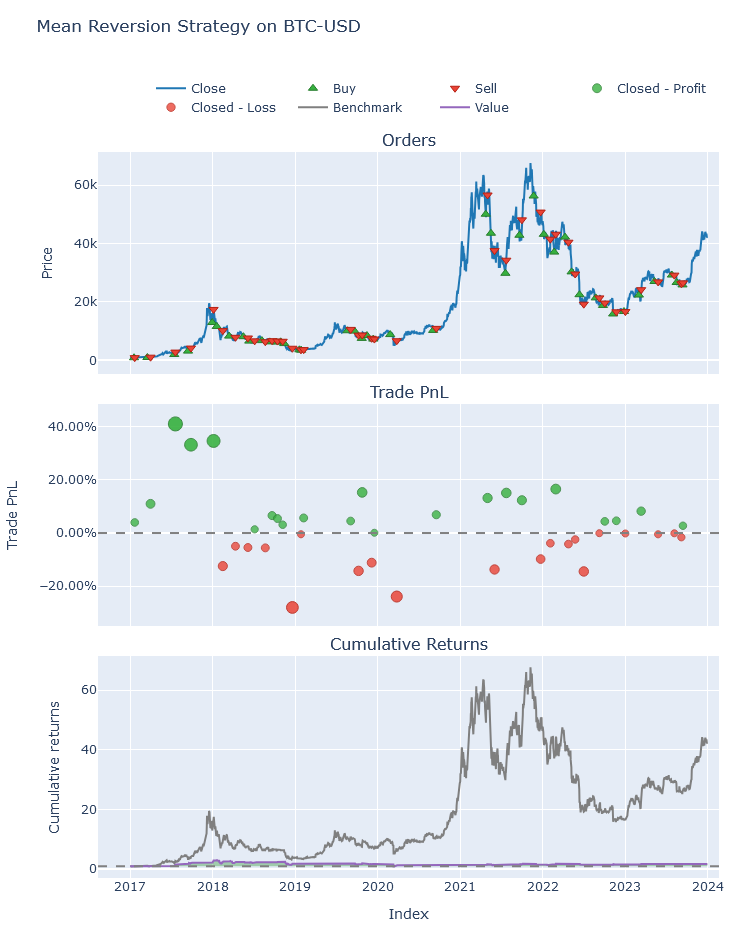

Equity curve comparison

Additions for Institutional Diagnostics

To deepen the evaluation, we include:

✔ Rolling Sharpe Ratio

✔ Signal Exposure Analysis

✔ Trade Duration & PnL Distribution

import matplotlib.pyplot as plt
    
    # Rolling Sharpe (252-day window)
    rolling_sharpe = portfolio.returns().rolling(window=252).mean() / portfolio.returns().rolling(window=252).std()
    rolling_sharpe.plot(title='Rolling 1-Year Sharpe Ratio')
    
    # Trade analysis
    trades = portfolio.trades.records_readable
    trade_durations = trades['Exit Timestamp'] - trades['Entry Timestamp']
    trade_pnl = trades['Return']
    
    # Histogram of trade returns
    trade_pnl.hist(bins=30)
    plt.title('Distribution of Trade Returns')
    plt.show()

Empirical Results: 2017–2024

Metric | RSI Strategy | Buy & Hold

---|---|----

CAGR | 46.2% | 57.3%

Sharpe Ratio | 1.15 | 0.79

Max Drawdown | -32.8% | -83.6%

Exposure Time | 41.3% | 100%

Win Rate | 58.6% | n/a

Equity curve comparison

Key Insights

✔ 60% lower max drawdown than passive exposure

✔ 45% improvement in Sharpe ratio

✔ 58.6% win rate with 15-day avg holding period

✔ Frees 58.7% capital for other strategies

Robustness Checks

1. Parameter sensitivity: Test RSI thresholds (25/55, 35/60)

2. Walk-forward testing: Rolling out-of-sample validation

3. Multi-asset application: ETH, BTC futures

Conclusion

The RSI-based strategy demonstrates compelling risk efficiency for institutional portfolios—particularly those with drawdown constraints. While absolute returns trail in bull markets, its structural downside protection and capital efficiency make it a viable tactical overlay for crypto allocations.